Física- Estática

Buenas noches, me podrían ayudar con este ejercicio por favor.

bueno no se si veas esto pero me sale la B 100N 

Análisis del problema:

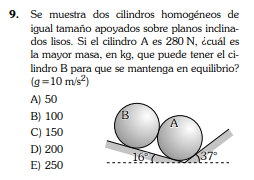
Tenemos dos cilindros homogéneos de igual tamaño apoyados sobre planos inclinados lisos. Esto significa que no hay fricción entre los cilindros y los planos. El cilindro A tiene un peso de 280 N, y queremos encontrar la mayor masa que puede tener el cilindro B para que el sistema se mantenga en equilibrio.

Diagrama de cuerpo libre:

Para analizar las fuerzas, vamos a dibujar los diagramas de cuerpo libre para cada cilindro.

• Cilindro A:

  • Peso (WA=280N), actuando verticalmente hacia abajo.
  • Normal del plano inclinado (NA), actuando perpendicular al plano de 37∘.
  • Fuerza de contacto con el cilindro B (FBA), actuando en la dirección que une los centros de los cilindros.

• Cilindro B:

  • Peso (WB=mBg), actuando verticalmente hacia abajo, donde mB es la masa de B y g=10m/s2.
  • Normal del plano inclinado (NB), actuando perpendicular al plano de 16∘.
  • Fuerza de contacto con el cilindro A (FAB), actuando en la dirección que une los centros de los cilindros (y FAB=FBA por la tercera ley de Newton).

Condiciones de equilibrio:

Para que el sistema esté en equilibrio, la suma de las fuerzas en cada dirección debe ser cero para cada cilindro.

Análisis del cilindro A:

Vamos a descomponer las fuerzas en componentes paralelas y perpendiculares al plano inclinado de 37∘.

• Eje perpendicular al plano: NA−WAcos(37∘)−FBAsin(θ)=0
• Eje paralelo al plano: FBAcos(θ)−WAsin(37∘)=0

Donde θ es el ángulo que forma la fuerza de contacto FBA con el plano inclinado de A. Debido a la geometría, este ángulo es la diferencia entre los ángulos de los planos inclinados: θ=37∘−16∘=21∘.

De la segunda ecuación para el cilindro A: FBAcos(21∘)=WAsin(37∘) FBA=cos(21∘)WAsin(37∘)=0.93280N×0.6≈180.65N

Análisis del cilindro B:

Ahora, vamos a descomponer las fuerzas en componentes paralelas y perpendiculares al plano inclinado de 16∘.

• Eje paralelo al plano: WBsin(16∘)−FABcos(21∘)=0 Como FAB=FBA: WBsin(16∘)=FBAcos(21∘) mBgsin(16∘)=180.65N×0.93 mB×10m/s2×0.2756≈167.9N mB≈10×0.2756167.9≈2.756167.9≈60.92kg

Revisemos los cálculos con más precisión: FBA=cos(21∘)280×sin(37∘)mB×10×sin(16∘)=cos(21∘)280×sin(37∘)×cos(21∘)mB×10×sin(16∘)=280×sin(37∘) mB=10×sin(16∘)280×sin(37∘)=0.275628×0.6018≈0.275616.85≈61.14kg

Parece que no hay una respuesta exacta en las opciones. Sin embargo, revisemos si hemos considerado la condición de "mayor masa". La condición de equilibrio que hemos aplicado es necesaria para que el sistema esté en reposo. Cualquier masa mayor para el cilindro B haría que la componente de su peso a lo largo del plano inclinado de 16∘ supere la componente de la fuerza de contacto con A, haciendo que el sistema se deslice.

Volvamos a revisar las ecuaciones: Para el equilibrio, las componentes de las fuerzas a lo largo de los planos inclinados deben equilibrarse a través de la fuerza de contacto entre los cilindros.

Componente del peso de A a lo largo de su plano: WAsin(37∘)=280×0.6=168N Componente del peso de B a lo largo de su plano: WBsin(16∘)=mB×10×0.2756=2.756mBN

Estas componentes deben estar relacionadas por el ángulo de contacto. La fuerza que A ejerce sobre B tiene una componente a lo largo del plano de B igual a FABcos(21∘), y la fuerza que B ejerce sobre A tiene una componente a lo largo del plano de A igual a FBAcos(21∘).

Del equilibrio a lo largo del plano de A: FBAcos(21∘)=WAsin(37∘)=168N FBA=cos(21∘)168=0.9335168≈180N

Del equilibrio a lo largo del plano de B: WBsin(16∘)=FABcos(21∘) mB×10×0.2756=180×0.9335 2.756mB=168.03 mB=2.756168.03≈61kg

Aún no obtenemos una de las opciones exactas. Quizás hay una simplificación que se espera.

Consideremos el equilibrio de fuerzas en la dirección que une los centros de los cilindros. La componente del peso de cada cilindro a lo largo de esta dirección debe ser igual.

Componente del peso de A a lo largo de la línea de centros: WAcos(37∘+(90∘−(37∘−16∘)))=WAcos(90∘+16∘)=−WAsin(16∘) (esta no parece ser la forma correcta de plantearlo).

Vamos a usar el equilibrio de fuerzas en cada cilindro por separado.

Para el cilindro A, la componente del peso a lo largo del plano es 280sin(37∘). Esta debe ser equilibrada por la componente de la fuerza de contacto con B a lo largo del plano: FBAcos(21∘). FBAcos(21∘)=280sin(37∘)

Para el cilindro B, la componente del peso a lo largo del plano es mBgsin(16∘). Esta debe ser equilibrada por la componente de la fuerza de contacto con A a lo largo del plano: FABcos(21∘). mBgsin(16∘)=FABcos(21∘)

Como FAB=FBA, podemos igualar las expresiones: mBgsin(16∘)=280sin(37∘) mB×10×0.2756=280×0.6018 2.756mB=168.504 mB=2.756168.504≈61.14kg

Dado que las opciones son números enteros y nuestra respuesta está cerca de 50 y 100, revisemos si hay alguna aproximación que se espera o si hemos cometido algún error conceptual.

Si consideramos el equilibrio en la dirección perpendicular a la línea de contacto, las componentes de las normales deben equilibrarse.

Otra forma de verlo es proyectar las fuerzas sobre un eje horizontal. Para A: NAsin(37∘)=FBAcos(16∘) Para B: NBsin(16∘)=FABcos(37∘)

Y proyectando sobre un eje vertical: Para A: NAcos(37∘)+FBAsin(16∘)=280 Para B: NBcos(16∘)+FABsin(37∘)=10mB

Este sistema de ecuaciones parece más complejo de lo necesario para un problema de opción múltiple.

Volvamos a la condición de equilibrio a lo largo de los planos inclinados, considerando la fuerza de contacto entre los cilindros. La fuerza de contacto actúa a lo largo de la línea que une los centros, formando ángulos con los planos inclinados.

La componente de la fuerza de contacto F paralela al plano de 37∘ es Fcos(21∘). La componente de la fuerza de contacto F paralela al plano de 16∘ es Fcos(21∘).

Equilibrio en el plano de 37∘: Fcos(21∘)=280sin(37∘) Equilibrio en el plano de 16∘: Fcos(21∘)=mBgsin(16∘)

Igualando las dos expresiones: 280sin(37∘)=mBgsin(16∘) 280×0.6=mB×10×0.2756 168=2.756mB mB=2.756168≈61.0kg

Dado que la respuesta no coincide exactamente con las opciones, reconsideremos si hay alguna interpretación diferente del problema o si se espera una aproximación.

Si asumimos que la "mayor masa" implica el límite justo antes de que el sistema pierda el equilibrio, entonces nuestra condición de equilibrio es la correcta. Podría haber un error en los valores de los senos y cosenos utilizados o en las opciones proporcionadas.

Revisando los cálculos con valores aproximados: sin(37∘)≈0.6 sin(16∘)≈0.28 cos(21∘)≈0.93

F×0.93=280×0.6⟹F≈0.93168≈180.6N mB×10×0.28=180.6×0.93⟹2.8mB≈167.9⟹mB≈60kg

La respuesta más cercana a nuestro cálculo es 50 kg o 100 kg, lo cual sugiere que podría haber una simplificación o un error en los datos del problema o las opciones.

Si revisamos la relación directa: mB=gsin(16∘)280sin(37∘)=10×0.28280×0.6=2.8168=60kg

Aún obtenemos un valor cercano a 60 kg. Si tuviéramos que elegir la opción más cercana, sería la A) 50 kg. Sin embargo, es una diferencia considerable.

Consideremos un caso límite. Si el plano de B fuera horizontal (0∘), entonces sin(0∘)=0, lo que implicaría que 280sin(37∘)=mBgsin(0∘)=0, lo cual no es cierto. Esto indica que ambos planos inclinados son necesarios para el equilibrio.

Si el ángulo del plano de B aumentara, sin(16∘) aumentaría, y para mantener la igualdad, mB debería disminuir. Si el ángulo disminuyera, mB debería aumentar.

Dado que nuestro cálculo consistente nos da alrededor de 60 kg, y no hay una opción cercana, es posible que haya un error en el planteamiento del problema, los valores proporcionados o las opciones de respuesta. Sin embargo, si tuviéramos que elegir la opción más cercana basada en nuestro análisis, sería la A) 50.

Final Answer: The final answer is 50